Bivariate Probability Distributions
-
Definition and Marginal Distributions
-
Discrete
A discrete bivariate distribution represents the joint probability distribution of a pair of random variables. For discrete random variables with a finite number of values, this bivariate distribution can be displayed in a table of m rows and n columns. Each row in the table represents a value of one of the random variables (call it X) and each column represents a value of the other random variable (call it Y). Each of the mn row-column intersections represents a combination of an X-value together with a Y-value. The following table is the bivariate probability distribution of the random variables X=total number of heads and Y=toss number of first head (=0 if no head occurs) in tossing a fair coin 3 times. The numbers in the cells are the joint probabilities of the x and y values. For example P[X=2 and Y=1] = P[X=2,Y=1] = 2/8. The function f(x,y) = P[X=x,Y=y] for all real numbers x and y is the joint probability distribution of X and Y.
Y Values X Values 0 1 2 3 0 1/8 0 0 0 1 0 1/8 1/8 1/8 2 0 2/8 1/8 0 3 0 1/8 0 0
Notice that the sum of all probabilities in this table is 1. Since f(x,y) is a probability distribution, it must sum to 1. Adding probabilities across the rows you get the probability distribution of random variable X (called the marginal distribution of X). Adding probabilities down the columns you get the probability distribution of random variable Y (called the marginal distribution of Y). The next display shows these marginal distributions.Y Values X Values 0 1 2 3 0 1/8 0 0 0 1/8 1 0 1/8 1/8 1/8 3/8 2 0 2/8 1/8 0 3/8 3 0 1/8 0 0 1/8 1/8 4/8 2/8 1/8 The main property of a discrete joint probability distribution can be stated as the sum of all non-zero probabilities is 1. The next line shows this as a formula.
The marginal distribution of X can be found by summing across the rows of the joint probability density table, and the marginal distribution of Y can be found by summing down the columns of the joint probability density table. The next two lines express these two statements as formulas.
-
Continuous
A continuous bivariate joint density function defines the probability distribution for a pair of random variables. For example, the function f(x,y) = 1 when both x and y are in the interval [0,1] and zero otherwise, is a joint density function for a pair of random variables X and Y. The graph of the density function is shown next.
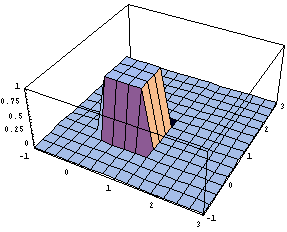
To find P[a<X<b,c<Y<d] integrate the joint density function of random variables X and Y over the region specified by the inequalities a<X<b and c<Y<d. For the case of the the joint density function shown above, integration amounts to finding volumes above regions in the xy plane. For example, P[1/2<X<1,1/4<Y<3/4] is found by finding the volume of the solid of constant height 1 above the region in the xy plane 1/2<X<1 and 1/4<Y<3/4. This region has area (1/2)(1/2), so the volume, and thus P[1/2<X<1,1/4<Y<3/4] = (1)(1/2)(1/2) = 1/4.
A bivariate continuous density function satisfies two conditions that are analogous to those satisfied by a bivariate discrete density function. First f(x,y) is nonnegative for all x and y, and second
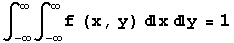
Also, like the bivariate discrete case, marginal continuous densities for random variables X and Y can be defined as follows:
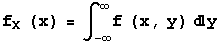
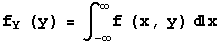
-
To Top
-
Conditional Probability
-
Discrete
In the discrete case conditional probabilities are found by restricting attention to rows or columns of the joint probability table. For example, the table below shows the joint probabilities of random variables X and Y defined above. The marginal probabilities are also shown. To find, for example, P[X=1 | Y=2], you simple need to look at the column of the table where Y=2. Then P[X=1 | Y=2] = P[X=1,Y=2]/P[Y=2] = (1/8)/(2/8) = 1/2. Any conditional probability for a pair of discrete random variables can be found in the same way.
Y Values X Values 0 1 2 3 0 1/8 0 0 0 1/8 1 0 1/8 1/8 1/8 3/8 2 0 2/8 1/8 0 3/8 3 0 1/8 0 0 1/8 1/8 4/8 2/8 1/8 -
Continuous
The technique shown above for a conditional probability in the discrete case doesn't carry over to the continuous case because the 'row' (the probability of a specific value of X) and 'column' (the probability of a specific value of Y) totals are zero in the continuous case. In fact, the joint probability of a specific value of X and a specific value of Y is zero. The approach taken to get around this limitation is to define conditional probability density functions as follows:
The conditional probability density function for X given Y=y is defined as
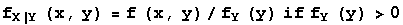
and fX|Y(x,y) is 0 where fY(y) = 0. The conditional probability density function for Y given X=x is given by
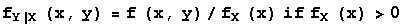
and fY|X(x,y) is 0 where fX(x) = 0.
An example of a conditional density computation comes from exercise 5.8 on page 271 of your textbook in which you are asked to compute P[X1 > 1/2 | X2 = 1/4]. To avoid subscripts, the example will be done here using X in place of X1 and Y in place of X2. Then the probability to be found can be written P[X > 1/2 | Y = 1/4]. From exercise 5.8 in that section, the joint density function of X and Y is f(x,y) = 2 when x is on the interval [0,1], y is on the interval [0,1], and x+y is on the interval [0,1]. The region over which this density function is nonzero is shown within the triangle below (the x axis is horizontal and the y axis is vertical).
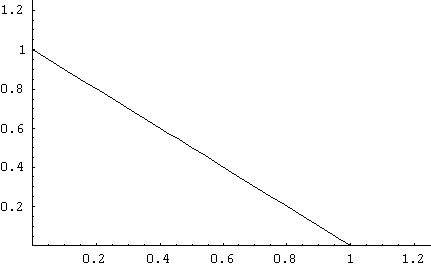
The conditional density function fX(x,y) = f(x,y)/fY(y), and fY(y) is found by integrating the joint density function from 0 to 1-y. This gives fY(y) = 2(1-y) for y on [0,1] and 0 otherwise.
Then fX|Y(x,y) = f(x,y)/fY(y) = 2 / (2(1-y)) = 1 / (1-y) for y between 0 and 1 and x between 0 and 1-y. Then P[X > 1/2 | Y = 1/4] is the integral of 1/ (1 - (1/4)) = 4/3 from 1/2 to 3/4. This equals ((3/4)-(1/2))(4/3) = (1/4)(4/3) = 1/3.
-
To Top
Recall that events A and B are independent if and only if P[A and B] = P[A] P[B].
For discrete random variables, the condition for independence of X and Y becomes X and Y are independent if and only if P[X=x,Y=y] = P[X=x] P[Y=y] for all real numbers x and y. This definition of independence for discrete random variables translates into the statement that X and Y are independent if and only if a cell value is the product of the row total times the column total.
Are the random variables X and Y described above with the following joint probability density table independent?
| Y Values | ||||||
| X Values | 0 | 1 | 2 | 3 | ||
| 0 | 1/8 | 0 | 0 | 0 | 1/8 | |
| 1 | 0 | 1/8 | 1/8 | 1/8 | 3/8 | |
| 2 | 0 | 2/8 | 1/8 | 0 | 3/8 | |
| 3 | 0 | 1/8 | 0 | 0 | 1/8 | |
| 1/8 | 4/8 | 2/8 | 1/8 | |||
The random variables are not independent because, for example P[X=0,Y=1] = 0 but P[X=0] = 1/8 and P[Y=1] = 4/8.
For continuous random variables, the condition for independence of X and Y becomes X and Y are independent if and only if f(x,y) = fX(x) fY(y) for all real numbers x and y.
For the joint density function f(x,y) = 1 for x on [0,1] and y on [0,1] and 0 otherwise, the marginal density function of X, fX(x) = 1 for x on [0,1] and the marginal density function of Y, fY(y) = 1 for y on [0,1]. The marginal density functions can be multiplied together to produce the joint density function. Thus the random variables X and Y are independent.
To Top
-
Expected Values
-
Expected Values of Functions of Two Random Variables
The following two formulas are used to find the expected value of a function g of random variables X and Y. The first formula is used when X and Y are discrete random variables with pdf f(x,y).
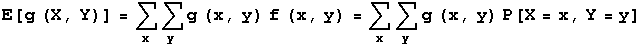
To compute E[X*Y] for the joint pdf of X=number of heads in 3 tosses of a fair coin and Y=toss number of first head in 3 tosses of a fair coin, you get
E[X*Y] = 0*0*(1/8) + 0*1*0 + 0*2*0 + 0*3*0 +
1*0*0 + 1*1*(1/8) + 1*2*(1/8) + 1*3*(1/8) +
2*0*0 + 2*1*(2/8) + 2*2*(1/8) + 2*3*0 +
3*0*0 + 3*1*(1/8) + 3*2*0 + 3*3*0 = 17/8
The next formula is used when X and Y are continuous random variables with pdf f(x,y).
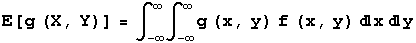
In computing E[X - Y] for the random variables X and Y whose joint pdf is 1 for x in [0,1] and y in [0,1] and 0 otherwise, you get the following.
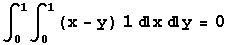
-
Covariance and Correlation of Two Random Variables
The covariance is a measure of association between values of two variables. If as variable X increases in value, variable Y also increases, the covariance of X and Y will be positive. If as variable X increases in value, variable Y decreases, the covariance of X and Y will be negative. If as X increases, there is no pattern to corresponding Y-values, the covariance of X and Y will be close to zero. The covariance of X and Y are defined as follows.
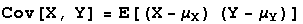
where the subtracted terms are the expected value of X and the expected value of Y, respectively. You will usually want to use the equivalent formula Cov[X,Y] = E[XY] - E[X]E[Y] to compute covariance of X and Y.
For example, the covariance for the discrete random variables X and Y defined above, it has been shown that E[XY] = 17/8. From the marginal pdf of X, you get E[X] = 3/2, and from the marginal pdf of Y, you get E[Y] = 11/8. Then Cov[X,Y] = (17/8) - (3/2)(11/8) = 17/8 - 33/16 = 34/16 - 33/16 = 1/16.
Using covariance to measure the degree of association between two random variables is flawed by the fact that covariance values are not restricted to a real number interval. This flaw is overcome by using the correlation coefficient for two random variables. The correlation coefficient is a normalized form of covariance whose values are restricted to the interval [-1,1].
The correlation coefficient of random variables X and Y is given by
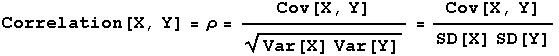
For random discrete random variables X=number of heads in 3 tosses of a fair coin, and Y=toss number of first head in 3 tosses of a fair coin, Var[X] = E[X2]-(E[X]2) = (24/8) - (3/2)2 = (24/8) - (18/8) = 6/8 = 3/4 and Var[Y] = E[Y2]-(E[Y]2) = (21/8) - (11/8)2 = (168/64) - (121/64) = 47/64. Then the correlation for X and Y is (1/16)/((3/4)1/2(47/64)1/2) = 0.08. Thus these two random variables have a weak positive association.
Finally, a result for computing expected values and variances for linear combinations of random variables. If X1,X2,...,Xn are random variables, a linear combination of them is the sum a1X1+a2X2+...+anXn where a1,a2,...,an are constants. The following statements show how expected values and variances of these linear combinations are computed.
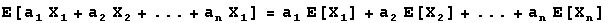
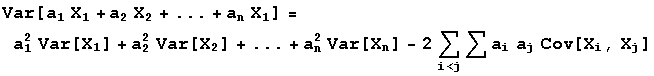
-
To Top
-
The Multinomial Distribution
-
Definition
Most of the discrete random variables studied in earlier chapters were based on a model in which an experiment that could have two outcomes, success, with probability p, or failure, with probability q=1-p, was repeated a number of times. It was also assumed that outcomes on any run of the experiment were independent. Random variables considered under these assumptions were the Bernoulli, Binomial, Geometric, and Negative Binomial, and since the Poisson is a limiting form of a Binomial, in some sense, the Poisson.
The multinomial random variable generalizes the situation described in the first paragraph by allowing more than one two outcomes on each run of the experiment. If you think of tossing a coin as the model for the random variables described in the last paragraph, tossing a die is a good model for the multinomial random variable. If you toss the coin n times, you might want to record the number of 1's, the number of 2's, etc., through the number of 6's. If the die is fair, p1=probability of a 1 on any toss=1/6, p2=probability of a 2 on any toss=1/6,...,p6=probability of a 6 on any toss=1/6. The random variables Y1=number of 1's in n tosses of a fair die, Y2=number of 2's in n tosses of a fair die, ..., Y6=number of 6's in n tosses of a fair die have a multinomial distribution with parameters n, p1,p2,p3,p4,p5,p6.
-
Simulation
You can simulate multinomial random variables on a computer by dividing the interval [0,1] into k subintervals where k is the number of different possible outcomes. For example to simulate the tossing of a die, have the computer generate a uniform random variable on [0,1]. Divide [0,1] into subintervals [0,1/6], (1/6,2/6],(2/6,3/6], (3/6,4/6],(4/6,5/6],(5/6,1]. If the number falls into the first subinterval, a 1 has been tossed, if the number falls into the second subinterval, a 2 has been tossed, etc.
-
Probability Distribution
The probability distribution of the multinomial with parameters n, p1,p2,p3,p4,p5,p6 is
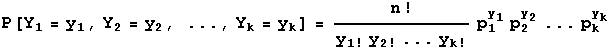
where y1+y2+...+yk=n and p1+p2+...+pk=1.
As an example, in tossing a fair die 30 times, the probability of five 1's, twelve 4's, and thirteen other numbers is given by a multinomial where Y1=number of 1's, Y2=number of 4's and Y3=number of other numbers. This multinomial distribution has parameters 30, 1/6, 1/6, and 4/6, and from the formula above the probability is
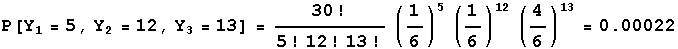
-
Expected Value and Variance
-
Expected Values
Each of the k random variables, Y1 through Yk has an expected value. To find the expected value of Y1 think of an outcome of type 1 as a success and all other outcomes as failures. The probability of a success is p1 and the experiment is repeated n times. This fits the model of a binomial random variable. The expected value of a binomial random variable is np. Thus the expected value of random variable Y1 is np1, and in general E[Yi]=npi.
-
Variance
The variance of Yiis found by thinking of Yi as you do in computing the mean. Since the variance of a binomial random variable is npq, the Var[Yi]=npi(1-pi).
-
Covariance of Yi and Yj
As you might imagine, the random variables in a multinomial distribution are related. As example if you throw a die 10 times and Y1 is the number of 1's, Y2 is the number of 4's, and Y3 is the number of other numbers in the 10 throws of the die, larger values of Y1 will force smaller values of Y2 and Y3. This relationship implies a negative covariance for any pair of the random variables. It can be shown that Cov[Yi,Yj]= -npipj.
-
-