• Statistics that Measure Central Tendency

  • Mean

    Your have probably used the mean since elementary school.  There it is was called the average.  The mean (or average) of a collection of numbers is computed by adding the numbers and dividing by the number of numbers.  For example the mean of the numbers 2,3,3,4,5,6 is 23/6=3.8 rounded to the nearest tenth.  In formula form, the mean of n numbers, x₁, x₂, ..., x_n is given by the sum of the x's divided by n, the number of x's, or

    

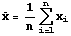
    For a data set presented as numbers together with the frequency of occurrence of each number, as in the next table, the computation of the mean is slightly modified.

    Number	Frequency
    2	2
    3	6
    4	7
    5	3
    7	3
    9	2

    Add another column consisting of each number multiplied by the frequency of occurrence of that number to the table.  Then find the sum of this column as shown:

    Number	Frequency	Number*Frequency
    2	2	4
    3	6	18
    4	7	28
    5	3	15
    7	3	21
    9	2	18
    Sum of (Numbers*Frequencies)=		104

    The mean is the (Sum of Numbers*Frequencies)/(Sum of Frequencies).  In the example the sum of the frequencies is 23, so the mean is 104/23=4.5.  In formula form, the mean of numbers x₁which occurs with frequency f₁, x₂ which occurs with frequency f₂, etc., up to and including x_n which occurs with frequency f_n is given by

    

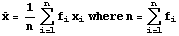
    The mean is easy to compute, and as mentioned above, you have probably used it before, but it has one major drawback--it is severely affected by extreme values.  For example the mean of 2,3,4,5, and 6 is 4.  However, if another number, say 20, is added to the set, the mean of the new set of numbers, 2,3,4,5,6, and 20 is now 40/6=6.7.  Certainly the mean should increase but increasing from 4 to 6.7 might be considered to be too much of a change.

    In presenting housing prices in the newspaper the mean price of a home will not be used, simply because the mean is overly affected by the few very expensive homes in a typical community.  The median price of a home is usually printed.  The next section discusses the median.

     

  • Median

    The median of a collection of numbers is in some sense the 'middle' number of that set.  For example the median of the numbers 2,3,4,5,8 is 4 because 4 is the 'middle' number.  What is the median of the numbers 2,3,4,5,8,10?  Here the median is the average of the two middle numbers, 4 and 5.  The median is then (4+5)/2=4.5.

    The process for computing the median of a set of n numbers is:

    • Sort the numbers and arrange them from smallest to largest.

    • Consider the smallest number to be in position 1, the next number in the sorted list to be in position 2, the next in position 3, etc.

    • The median will be the number in position (n+1)/2.  If (n+1)/2 is a whole number, the median will be the number lying in that position.  If (n+1)/2 is a fraction, say 7.5, the median will be the average of the two numbers in positions 7 and 8.

    Example: Find the median of the numbers 2,3,1,4,4,5,7,2,3, and 8.

    • In sorted order the numbers are 1,2,2,3,3,4,4,5,7,8

    • The numbers with their positions are

      Position	1	2	3	4	5	6	7	8	9	10
      Number	1	2	2	3	3	4	4	5	7	8

    • The median is the number in position (10+1)/2=5.5.  Since 5.5 is not a whole number, the median is the average of the numbers in positions 5 and 6, or the average of 3 and 4 which equals 3.5.  The median is 3.5.

  • Mode

    The mode is the number that occurs most frequently.  For the set of numbers 2,3,4,5,5,6, the mode is 5.  The set of numbers 2,3,4,5,5,6,6 has two modes, 5 and 6.  It is bimodal.  However, when all numbers in a set occur with the same frequency, the set of numbers has no mode.  For example, the numbers 2,2,3,3,4,4,5,5 have no mode.

     

  • Quartiles and Percentiles

    The median divides a set of numbers into halves.  Quartiles divide a set of numbers into quarters and percentiles divide a set of numbers into hundredths.  You may have received scores on school achievement tests as percentile scores.  If you were told that you were at the 92nd percentile, then 92% of the test scores were equal or less than your score and 8% of the test scores were equal to or better than your score.

    There are three quartiles for a set of numbers, the 1st quartile, denoted by Q₁, the 2nd quartile

    denoted by Q₂, and the 3rd quartile denoted by Q₃.  The 2nd quartile is also called the median, and you have seen how to compute the median.  The quartiles divide the dataset into quarters.  To compute the 1st quartile, Q₁, simply find the median of all numbers in the dataset that are less than or equal to the median.  To compute the 3rd quartile, Q₃, find the median of all numbers in the dataset that are greater than or equal to the median.

    Position	1	2	3	4	5	6	7	8	9	10
    Number	1	2	2	3	3	4	4	5	7	8

    The median of the numbers in the table just above was found to be the average of the numbers in positions 5 and 6, that is (3+4)/2=3.5.  Then the 1st quartile is the median of the numbers that are less than or equal to 3.5, that is the median of 1,2,2,3,3.  These numbers are sorted and the positions are the same as in the last table.  Since there are 5 numbers, the median is the number in position (5+1)/2=3, and this number is 2.  Q₁=2.  The 3rd quartile is the median of the numbers greater than or equal to 3.5, or the median of 4,4,5,7,8.  Again, since there are 5 numbers here, the median of this set of 5 numbers is the number in position 3, that is 5.  Q₃=5.

     

  • Resources

A demonstration page for descriptive statistics showing the relationship between the histogram of a set of numbers and the corresponding descriptive statistics is found by following this link to a page designed by Eric Scheide.  The following display shows the page.

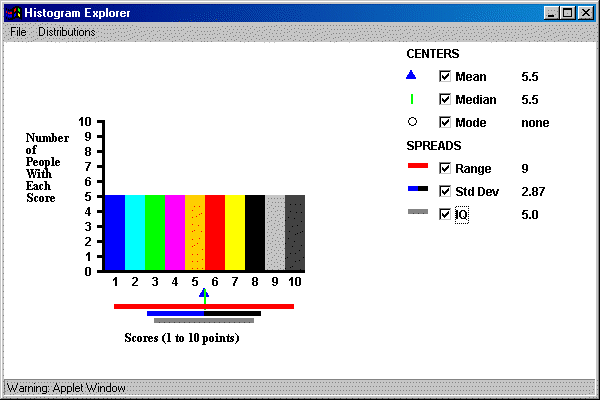
The Hyperstat Online pages also have a demonstration of means and medians related to a histogram of a set of numbers.  Follow this link to reach the pages on this topic.  Follow all of the links at the left of that page, ending this section by doing the exercises found there.

• Statistics that Measure Variability

  • Range

    The range of a set of numbers equals the largest number minus the smallest number.  The range of the numbers 3,5,9,9,10,13 is 13-3=10.  The range is affected by extreme or outlying numbers.  The next statistic, the interquartile range does not have this drawback.

     

  • Interquartile Range (IQR)

    The interquartile range is the third quartile minus the first quartile, IQR=Q₃-Q₁.  For the set of numbers 1,2,2,3,3,4,4,5,6,7, in the examples above Q₁ was found to be 2 and Q₃ was found to be 5.  Thus the interquartile range is 5-2=3.  Compare this with the range=7-1=6.

     

  • Standard Deviation

    The measure of variability used most often is called the standard deviation.  The standard deviation is roughly the average of squared deviations from the mean.  The formula for the standard deviation of  x₁, x₂, ...,x_n is  

    

    where x-bar is the mean of the numbers.

    As an example consider the numbers 2,3,4,5,6.  The mean is 4.  Then the differences between each of the numbers and the mean are (2-4)=-2, (3-4)=-1, (4-4)=0, (5-4)=1, and (6-4)=2, respectively.  The formula indicates that these numbers must be squared and added.  The squares are 4,1,0,1, and 4, and the sum is 10.  Finally the formula directs you to divide this sum by the number of numbers-1, i.e. n-1, and take the square root.  This results in the square root of 10/4 or the square root of 2.5 which is approximately 1.58. 

    The square of the standard deviation is called the variance of the set of numbers.  The variance has the drawback that the units of standard deviation are the square of the units of the numbers used to compute variance.  For example, if the units of the numbers shown in the last example are inches, the units of the variance are square inches.

     

    An easier formula for computing the standard deviation is

    

    and the easy formula for computing standard deviation for numbers, x_i, given along with frequencies, f_i, is

    

  To see a demonstration of these statistics link to a page designed by Eric Scheide or to this page from Hyperstat Online.

  
  

• Other Statistics
  

  • Standard Scores

    Suppose you and a friend are both taking a statistics class but are in different sections.  You both take a midterm examination and wish to compare your performances on the exam.  You received a score of 80 in a section that had a mean of 76 and a standard deviation of 5, while your friend received a score of 76 in a section that had a mean of 66 and a standard deviation of 8.  Who performed better?  In order to determine this, the scores need to be placed on the same footing, that is be modified as if they both came from a test with the same mean and standard deviation.  This can be done by subtracting the mean of the section and dividing by the standard deviation of the section.  That is (x-mean)/(standard deviation) is computed for each score.  For your score of 80 this results in (80-76)/5=0.8 while for your friend's score you get (76-66)/8=1.25.  This means that your friend had a better performance.

    The standard score corresponding to a number x, denoted by z, is given by the next formula:

    

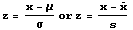
    where x is the actual score, x-bar is the mean of the set of numbers, and s is the standard deviation of the numbers.  The standard score indicates how many standard deviations above (if z is positive) or below the mean (if z is negative) the number, x, falls.

     

  • Sample and Population Statistics

    All of the statistics used above apply to samples--they are called sample statistics.  The related statistics for populations are slightly different.  The following notations and differences in formulas apply:

    • Descriptive measures for a population are called parameters of the population while related measures for a sample are called statistics of the sample.

    • The size of a sample is usually denoted by n while the size of the population is given by N

    • The sample mean is written as x-bar while the population mean is usually denoted by µ.

    • The sample standard deviation is called s and the population standard deviation is called sigma.

    • The formula for sample standard deviation is

      

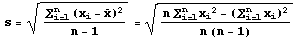
      but the formula for population standard deviation is

      

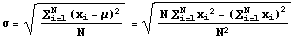
      There are two differences.  First, the sample mean is replaced by the population mean.  This isn't surprising.  The second difference, the divisor for the population standard deviation is N, while the divisor for the sample standard deviation is n-1 is harder to explain.  There is a good statistical reason for the difference but that reason will be left to another statistics course.  You should simply use the formula that is appropriate for the situation.