
The Algorithm Collection Project:
A Preliminary Report
on the Preliminary Findings Using the Ethnomathematics of Basic Number Sense
Acquisition
Daniel Clark Orey, Ph.D.
College of Education
California State University, Sacramento
Many people experience mathematics negatively. Many more students have
difficulty in performing basic arithmetic operations that may ultimately
exclude them from full participation in society (Moses, 2001). Comparable
populations across the world have fewer problems with mathematics than do
American students (TIMSS, 1997). Facility with the algorithm one uses ó
which includes its unique history and cultural significance, certainly contributes
to oneís success or failure in mathematics. As well, a fundamental
aspect of this project respects the importance of the complex interaction
between the languages spoken and the algorithms used that combine to form
individual abilities or disabilities in mathematics. Success during early
attainment of arithmetic operations forms the basis for how successfully one
learns advanced mathematics. Work with mathematics learners in other countries
(Orey, 2000, 1999, 1998, 1984), combined with the data gleaned from the Third
International Math Science Survey, suggests that true reform insuring successful
mathematics attainment for all is extremely complex. An in-depth study of
the type of algorithms used has important international significance as well.
An important goal of this project is to contribute data that will enable
the development of a viable working model for facility with basic mathematics
across cultures.
Project Design
The design of the project encompasses a three-step process:
Collection: Using an interview protocol developed by DíAmbrosio, Bassanezi, and Pompeu, Jr. (Orey & Rosa, 2001) the principle investigator (PI) trained new cohorts of graduate and preservice student teachers to interview recently arrived immigrant students (RAI) related to the attainment and use of the four basic facts in mathematics. The detailed nine-step modeling process is discussed below.
Analysis: Each semester, the PI interviews a selected sample of the collected RAI sample. A website will eventually share examples and interviews from subjects willing to share their stories and algorithms. The samples will be analyzed using interview data, for protocols, and error patterns distinctive to each algorithm and its ethnomathematical content. During the pilot study in an urban high school in Sacramento, California over 16 different nationalities were represented. The pilot study uncovered three major patterns for long division being used by RAI high school students. The future proposed project seeks to reconfirm this pattern, and will look for other patterns in relation to addition, subtraction and multiplication algorithms and the unique relationship to multilingualism.
Redevelopment: Pilot study data, was used to construct a new course
objective for preservice mathematics methods students. Students were asked
to interview a newly arrived immigrant. Future research seeks to catalog
and study methods used in basic standard arithmetic calculation. This new
data will enable this researcher to further study the cognitive consequences
inherent in culture, language and algorithms have for children.
Research Question and Significance
Do algorithms we use have cognitive, as well as pedagogical significance for their users? Recent research suggests that oneís mother tongue affects oneís personal form of cognitive processing (Holtz, 2001). It appears that some language groups have significantly more incidences of dyslexia, most notably native monolingual speakers of American English. This interaction of language and written language, suggests that American children may possess equal difficulty with the algorithms used. This may be influenced by factors related to unique linguistic interactions and the algorithms learned by millions of American school children. Educators in many countries are surprised to find that common day-to-day algorithms often differ by culture and by national origin.
For example, the pilot study data suggested that there may be at least
three major patterns used for long division. This researcher has collected
division algorithms used by newly arrived ninth graders in an urban public
high school, which fell into three major styles or patterns. For purposes
of this study they are called: North American; Franco-Brazilian;
and Russo-Soviet.
Context
Despite its downside, colonial interactions enabled different teaching styles to emerge in many former European colonies. The not always positive contact between cultures did however enable new ways of thinking and learning to emerge ó this seems especially true in North and South America. In the case of Brazil and the United States the unique mixtures of high-technology, languages and cultures contributes to a creative mix of new mathematical strategies and ideas.
In many places in the world, immigration and urbanization have brought together members of diverse cultures. For instance, the worldís third largest city, São Paulo, is also considered one of the largest Japanese speaking cities in the world. Besides being the worldís largest Portuguese-speaking city, its international stature makes it one of the largest English speaking cities as well. The same multicultural phenomenon occurs in other cities such as Tokyo, London, Los Angeles and New York. Globalization and an immerging international culture brings with it challenges as well as opportunities for educators and students alike. For example, some language groups use the coma for the decimal, which can cause for some confusion for scientists, business people, students and educators. Mistakes, often deadly, in translation between standard and metric measurements are legendary. Thus the a strong case can be made for studying "what works" across cultures in relation to number sense acquisition. What is a surprise to many educators is that there are other methods for learning, memorizing, calculating and communicating answers successfully that are currently used by people in other countries.
Much of what has been studied in both ethnomathematical and multicultural
contexts has often been related to the ancient ways of doing algorithms.
For example, it is not uncommon for textbooks in many countries, to introduce
Roman and Babylonian number systems, medieval-Russian peasant addition, Napierís
Bones and other such activities as historical curiosities. It is also quite
common to study certain aspects of Aztec-Mayan math (Orey, 1982). The Algorithm
Collection Project is innovative from an ethnomathematical perspective as
well, because it seeks to develop a new protocol for the applied study of
modern algorithms using modeling and an ethnomathematics perspective.
Background
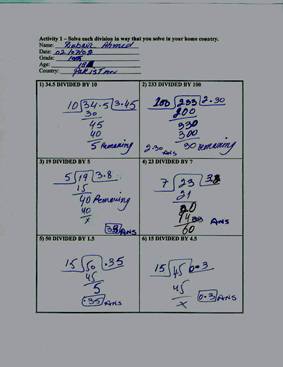
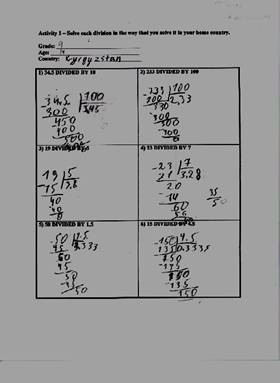
This study is built upon data collected, organized and developed in 1999 ó 2000 in an urban high school in Sacramento, California. A Brazilian graduate student, Mr. Milton Rosa, serving as a visiting foreign exchange teacher in mathematics, was having difficulty in using the standard North American algorithm and realized that his method also differed from that of a number of his students (see examples from Brazil and Kazakhstan). He asked his students representing 16 different countries, to demonstrate how they learned to do long division in their former schools. This proposal stems from the initial shared findings and early conversations with these ninth graders.
This project will enable a curriculum to be built that allows teachers to use, demonstrate and discuss alternative forms of calculation in such a way that the alternatives may be considered as different "remedies" administered to learners who did not respond to the "traditional treatment" or algorithm.
What is Ethnomathematics?
Ethnomathematics forms the intersection set between mathematics and cultural anthropology. The actual theory of ethnomathematics was introduced by Brazilian mathematician Ubiratan DíAmbrosio (2001, 1999, 1998, 1985) who explained that ethnomathematics is derived from "Techne, the art or technique; Mathema, that is to explain, to understand, of playing in reality; and Ethnos that which falls within or inside of a proper cultural context." Thus, ethnomathematics is the "art or technique of explaining reality within a proper cultural context." The term ethnomathematics is used to express the relationship between culture and mathematics. The term describes concepts that are themselves neither rigid nor singular ó namely, ethno and mathematics (DíAmbrosio, 1985; Powell & Frankenstein, 1997).
Mathematical Modeling
The construction of mathematical concepts incorporates the reality of each individual. This begins by placing new situations and problems in front of a child for them to master within their own context and experiential reality. It is on this basis that math concepts are learned. It is with a focus on the understanding and resolution of problems, that we "do" mathematics. Like all empowered users of mathematics, learners must be given experiences that enable them to learn how to mathematically:
This work within a mathematics reality is related to what Paulo Freire referred to as a "transforming action" (Freire, 1997). This action looks to reduce its degree of complexity through the choice of a model that it represents. In this isolated model, representations of this reality are derived by enabling the elaboration of strategies that explore, explain, and increase comprehension. This is why cross-cultural study of basic algorithms allows us to reflect on the inherent possibilities and for these same possibilities to become the object of critical analysis by the learners themselves. The process in which we consider, analyze and make ongoing reflections on different algorithms is called modeling.
In acquiring knowledge by using modeling, we work with approaches by which we construct representations. This can be done through analyses and reflections on various models, which end-up guiding this to become an extremely practical pedagogy. So it is that ethnomathematics has as its main objective the development of qualitative reflections and active participation by the learners themselves, so that they may be better able to trace parallels between their experiences and that of the out-of-school reality. Thus modeling fits into an evolving ethnomathematically-based program, because "it includes thinking in a critical and historical nature, and uses representations that must underlie the modeling process (DíAmbrosio, 1993)." An ethnomathematics-based pedagogy involves a transformation that manifests itself as action when questions are both formulated and answered by learners who are involved in the actual questions being posed, and can actively contribute to the direction of their own learning.
In making mathematics accessible for all students, educators must create conditions for increased involvement by all students (Orey, 1998, NCTM, 1999, Moses, 2001). Ethnomathematics suggests that modeling becomes a significant part of classroom pedagogy whereby good models are elaborated, demonstrated and shared freely, much like children do with computer game techniques. It goes without saying that students learn as they apply models and see mathematics as something practical if it is valuable to them. It is a "learn by doing" philosophy not unlike learning to play soccer or beat a computer game (Orey & Rosa, 2001). This form of modeling develops further models that are realistic, interesting and useful to students. Mathematical modeling is the study of problems or situations. It is a "language for understanding, simplification and resolution" with insights towards making possible forecasts or modifications of studied objects (Bassanezi, 1994). Ethnomathematics-based mathematical modeling is a learning strategy that values the childís knowledge and academic performance and is a form of pedagogical action. It discloses the latent possibilities inherent in mathematics by using modeling as a methodology (Orey & Rosa, 2001).
The way to introduce students to mathematical modeling is to expose them to a diversity of problems and models that include mathematical interpretations of problems, that in turn, are representations of models under study. When we analyze a given situation for its mathematical perspective, the teaching and learning process becomes more than an over emphasis on rote memorization of basic facts.
Mathematical questions are used to explain and to make forecasts on phenomena
in the real world. What is interesting from an ethnomathematics point of
view is that many of these explanations are unique from one culture to another.
This goes as well for algorithms that people use to make basic day to day
calculations. Many of these diverse perspectives are used in representing
situations for the study of alternative techniques used to make calculations.
By encouraging students to test their own ideas, students are connected
to the larger mathematical model by collaborating with them in the elaboration
of their own models. A detailed appreciation of hidden models (in this case
alternative algorithms) can then be made after the research is fully completed.
This can be done while assisting students with their ideas, and in elaboration
of the models they develop. The following procedures were developed for
mathematical modeling (Orey & Rosa, 2001) and were adapted for use in
this project:
1) Choice of a Subject
At the first stage, CSUS students were briefly introduced to multicultural aspects of algorithms. They were asked to find and contact a newly arrived immigrant to interview on a 1:1 basis. The choice of their interviewee was theirs as it was important that they are involved in the process themselves. The interviewers and the PI made use of a structured protocol, which will included a list of problems similar to those included here in the examples from the Marshall Islands, Brazil and Kazakhstan.
2) Research on a Subject
At this stage, the historical context of the study was developed. Besides discussing the actual algorithms, the interviewers were encouraged to find the context, which includes, but was not limited to, how the subject arrived in the United States, why their subject left their home country, information about how their subject learned mathematics, how the subject feels about mathematics instruction here and in their prior experience. The objective of this stage was the collection of the qualitative as well as the quantitative data to assist in the formulation of a hypothesis. In this case, the PI expected the interviewer to understand the intervieweeís story, as well as their method for calculation. This information was analyzed and interpreted by the PI as the foundation for the mathematical model. Both the PI and student interviewers collaborate in the construction of a database pivotal for subsequent phases of the project.
3) Question Elaboration
The questions considered are related to the interviewers and the content that they came to understand. Further considerations related to the relationship of the question with the problem were studied and considered at this time. The gathering of questions for the model was used to analyze and reflect upon in the subsequent stages.
4) Elaboration of the Mathematical Model
Here the interviewers needed a great deal of support by the PI who is intimately involved at this stage in the interpretation of the data. The PI organized and analyzed data collected by the interviewers. The study of these relationships was essential for understanding and getting to the "story" behind each algorithm and the user. This activity leads to formulating a hypothesis.
For example, from stories gleaned from the pilot study data, the interviewers were told repeatedly how much higher the expectations were for them by the schools, and how much more difficult the mathematics was in their home country. Many seemed mystified as to why American students have such difficulty with seemingly inconsequential details ó i.e. basic facts and algorithms. As well, it became apparent here that a number of newly arrived immigrants from Mexico, who are probably not "literate" in Spanish, and who were having a great deal of difficulty in learning English, were also having enormous difficulty in using standard American algorithms. When asked to explain in Spanish, and to use their algorithm, they perform more successfully at classroom activities and mathematical tasks that are with in their own contexts.
5) Formulating the Problems
As formulation of the studied algorithms appeared, the analysis of the data began with some unanticipated questions that arose, and include: Were there similar patterns in the other algorithms? Do new findings conform to any understood language and/or cultural patterns ó i.e. why does it appear that many multilingual students from the former Soviet Bloc have an easier time of adapting and learning than bilingual immigrants from Mexico and Central America? At this stage the PI did not have to clarify these questions related to the research subject but was ready to clarify the process itself, so that the interviewers could more easily organize their data, doubts and concerns, and ask further questions.
6) Resolution of the Mathematical Problems
This phase began the stage where the PI was able to design future activities for lessons teachers may use in the future testing phases of this project. The PI was careful to not over anticipate the difficulties related to the understanding of the cognitive as well linguistic challenges that the interviewers encounter.
7) Interpretation of the Solution
Coming to an understanding of how and why varied algorithms are used to calculate became clearer at this point of the modeling process. Ongoing discussions encouraged individual interviewers to reach an understanding of their findings through further exploration, study, refinement and interpretation of their own findings and solutions. This stage also allowed the PI to further refine ideas related to the development of curriculum activities to be tested in the later stage of this project.
8) Comparing the Model with Reality
At this stage the researchers compared their findings. When linguistic and culture models are found to be satisfactory, the PI used them to make the final analysis and moved towards completing the curricular activities that stemmed from this study.
9) Report, Defense and Evaluation of the Algorithms
At the end of each stage, interviewers shared results with their peers and the PI. Findings related to the stories, history, algorithms, the hypotheses and conclusions devised are shared.
10) Testing and Finalization
The above activities took place during much of the first and second semester of the project. The full study of this process will be devoted to the following activities: the ongoing collection and comparisons of collected algorithms, the further refinement of the interaction between cognitive and cultural aspects, and the development and testing of the curriculum modules in classrooms, a refinement of the data and website presentation.
Goals for Teachers and Students
As stated earlier, this project examined algorithms used by students coming
from a variety of diverse linguistic, historical, geographical and cultural
contexts. By bringing alternative strategies together, teachers and students
can learn to: flexibly solve problems, use alternatives when one strategy
does not work, and look at "best practices" from a global view. This project
gathered a modest representative sample of the basic arithmetic algorithms
used by peoples originating in diverse cultures. The data from this project
will be used to further refine this study and develop a number of curricular
strategies that can make use of this invaluable resource as found in this
community. As described above, this data will be used to develop a website
and course materials that enable educators to draw upon alternative forms
of calculating by making use of options or choices which are attuned to
diverse linguistic, cultural and cognitive abilities of individual students.
To facilitate ongoing interactions and contributions the future website
will be designed to be accessible in English, Spanish and Portuguese.
Reflections
A number of interesting things happened as an outgrowth from this activity. A few preservice students were extremely nervous about contacting someone to interview, "I do not know any one from another country" was heard a number of times. Together as a class group we brainstormed a number of possibilities for them which included:
Future additions to this activity will include:



Bibliography
Borba, M. (1990). "Ethnomathematics and education. " For The Learning of Mathematics 10(1).
Burns, M. (2000). About teaching mathematics: A K-8 resource. Sausalito, CA: Math Solutions Publications.
DíAmbrosio, U. (2001). "What is ethnomathematics, and how can it help children in schools?" In: Teaching Children Mathematics, 7(6). Reston, VA: National Council of Teachers of Mathematics.
_____________. (1999). Educação para uma sociedade em transição (Education for a Society in Transition). Campinas, SP, Brazil: Papirus Editora.
_____________. (1998). Ethnomathematics: the art or technique of explaining and knowing. International Study Group on Ethnomathematics: Las Cruces, NM.
_____________. (1985). "Ethnomathematics and its place in the history and pedagogy of mathematics. " For the Learning of Mathematics. 5(1): 44-48.
Freire, P. (1997). Pedagogia da Autonomia: Saberes Necessários à Prática Educativa (Pedagogy that Gives Autonomy: Necessary understandings towards a practical education). São Paulo: Editora Paz e Terra.
_______. (1987). Na Escola que Fazemos: Uma Refexão Interdisciplinar em Educação Popular (The school that we have made: an interdisciplinary reflection in education). Petrópolis: Editora Vozes.
_______. (1970). Pedagogia do Oprimido (Pedagogy of the Oppressed). São Paulo: Editora Paz e Terra S/A. 19 edição.
Holtz, R. L. (2001, March 16). "Study: Some written languages intensify dyslexia. " Sacramento Bee, p. A20.
International Study Group on Ethnomathematics (ISGEm) Website: http://www.rpi.edu/~eglash/isgem.htm
NCTM. (1999). Every child Statement. Reston, VA: National Council of Teachers of Mathematics (www.nctm.org).
Moses, R. (2001). Radical equations: Math literacy and Civil Rights. Boston: Beacon Press.
Orey, D. & Rosa, M. (2001). With Milton Rosa. Ethnomathematics as Pedagogical Action: Introducing Mathematical Modeling to Adolescent and Adult Learners. Unpublished manuscript, available from the authors.
Orey, D. (2000). "Etnomatemática como Ação Pedagógica: Algumas Reflexões sobre a Aplicação da Etnomatemática entre São Paulo e Califórnia (Ethnomathematics as Pedagogical Action: Some Reflections on Applying Ethnomathematics in São Paulo and California). " in Proceedings of the Primeiro Congresso Brasileiro de Etnomatématica ó CBEm1. Universidade de São Paulo, São Paulo, Brazil.
______. (1999). "Fulbright Ethnomathematics in Brazil. " International Study Group on Ethnomathematics Newsletter. Las Cruces: ISGEm, 14 (1).
______. (1998). "Mathematics for the 21st Century. " In: Teaching Children Mathematics, Reston, VA: National Council of Teachers of Mathematics.
______. (1989). "Ethnomathematical perspectives on the NCTM Standards. " International Study Group on Ethnomathematics Newsletter. 5(1): 5-7.
______. (1984). "Logo goes Guatemalan: an ethnographic study. " The Computing Teacher, 12(1): 46-47.
______. (1982). "Mayan Math. " The Oregon Mathematics Teacher. Portland, OR.
Parker, R. (1993). Mathematical Power: Lessons from the Classroom. New York: Heinemann.
Powell, A. B. and Frankenstein, M. Eds. (1997). Ethnomathematics: challenging eurocentrism in mathematics education. Albany, NY: State University of New York Press.
TIMSS. (1997). Third International Mathematics and Science Survey. See http://nces. ed. gov/timss.