The Interrelation of Language and Algorithms Used by Immigrants to Northern California

The Interrelation of Language and Algorithms Used by Immigrants to Northern California

This discussion traces the author’s the relationships of culture, social class, the language(s) spoken, and the particular algorithms used by recently arrived immigrants to Northern California. The study, undertaken in a diverse urban inner-city high school uncovered relationships among monolingualism, bilingualism and multilingualism, the algorithms used by these students, and their ability and self-confidence in overall mathematics. As a consequence of this study, The Algorithm Collection Project was established at California State University, Sacramento.

Bi-national students may come to school having learned different algorithms for the number operations than are commonly taught in the United States - Walter Secada

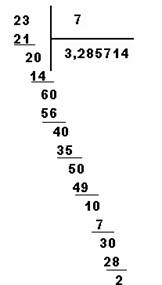
This investigation began when as a frequent classroom volunteer in a multilingual SDAIE[1] high school mathematics class. A mathematically high performing and confident young lady from the Ukraine asked me for one of the classroom calculators to perform a seemingly very easy division problem. I was mystified by this and so with help from the classroom translator[2] I inquired why she needed a calculator for this problem. I realized then that she was in need of it to find a square root. It was at that moment I recognized for the first time; the square root and the standard US long division sign can be confounded by newly arrived immigrant students from the former Soviet Union and South America (see Table 2 below).

Most readers are familiar with the worldwide historical processes of immigration and urbanization that have brought together cultures from every part of the world to places such as California, where many people do not yet speak the language of their new country[3]. A great need for teachers to learn and understand the problems and challenges of their immigrant students, and assist them to learn English; to interact and succeed in school is evident. Many immigrant students often come from monocultural contexts[4] and the diversity found here can be overwhelming. As well, the immigration brings with it opportunities for native-born students and educators to learn about cultural diversity as well as the “best” practices that people may bring with them. Within this context, an inordinately large number of native-born monolingual students in our region experience mathematics negatively. Many of these same adolescents possess difficulty in performing basic arithmetic operations that may ultimately exclude them from participation in society. We have the need for newly arrived immigrant students to understand their new cultural context, while at the same time not forgetting or devaluing their own. At the same time, this interaction can offer native-born students the opportunity to improve their own ability in mathematics.

Why is culture important in a mathematical context? A fundamental aspect of ethnomathematics is that culture influences what many have traditionally seen as a universal mathematics. For the purposes of this study, the concept of culture is linked to diversity, as “the diverse ways of being, knowing and doing” (Johnson, 2003, p. 4). These diverse ways of being, knowing and doing have come to influence the knowing and doing of mathematics is again fundamental to an ethnomathematics perspective.

Much of what has been studied in both historical and multicultural contexts of mathematics has often been related to the ancient ways of doing algorithms. For example, it is not uncommon for our textbooks to introduce Roman and Babylonian number systems, medieval-Russian peasant addition, Napier’s bones and other such activities as games, or historical curiosities. It is also common to use certain aspects of Aztec-Mayan mathematics as connections for history and multiculturalism in the mathematics classroom. Researchers have focused on bilingual elementary English/Spanish students, but little has been done through interviewing adolescent immigrants other than Spanish speaking children in the USA (Perkins & Flores, 2002; Philip, 1996). However, incidences in which researchers have documented the algorithms used by modern, urban, diverse populations in combination with their unique mix of culture could not be found in the literature.

One important aspect of public schools in Northern California is the large number of and diversity in the newly arrived immigrant population. For purposes of this study we have grouped this population into three categories as they learn both math and English:

Monolingual: People who can speak one language, that is they come to us as monolinguals (with various levels of fluency) and are now learning English and mathematics,

Bilingual: People who come to us as bilinguals (with various levels of fluency in both languages they can speak) and are now learning English and mathematics,

Multilingual: Or people who come to us with the ability to communicate in more than two or three languages (also with various levels of fluency) and are learning English and mathematics.

Many of the immigrants to our region of the world can be contrasted to the “native born” Californians who are, for most part, monolingual[5]. What interests this writer is the relationship between mono-, bi- and multilingualism, the particular algorithms they use and how well these students perform and their ease in new problem situations.

Interviews and observations here incorporated in this work with immigrant students in SDAIE mathematics classes, in order to ascertain each learner’s ability and/or disability, or facility in learning mathematics and how it relates to their language or language ability. I looked at how they performed on tests, group problems, and their overall academic performance, including an assessment of on-task classroom behavior. It is with this focus on the understanding and resolution of problems that the "doing" of mathematics across cultures took on special meaning for use with the students in this study sample. The students’ abilities to solve mathematical problems, in this school differ noticeably by culture, social class, and, as we have found, is generally influenced by the language(s) that are spoken. To the point that teachers’ expectations of different linguistically grouped students is equally noticeable at this school.

Because the students are 15 years and older in the math classes studied, there is no need to re-teach American standard algorithms, which was typically done in the past, or is done to younger immigrant students in the same school district. This research takes place in this context because the teacher takes particular care to create an environment of inquiry and openness that allows his students to share with the class as a whole their particular methods of calculation. As the students gain fluency in English, the students are free to share their ideas and work in their native languages. Both the teacher and I speak Portuguese and Spanish. In the case, where students speak other languages, the school has translators of Russian, Ukraine, Arabic, Farsi, Rumanian, and Cantonese. The teacher uses activities that enable opportunities for learning and practicing English in a mathematical context through the use of open-ended explorations, projects, group and individual assignments, through discussion and practice using a variety of mathematical methods, tools, and techniques, and by use of the vocabulary wall (see photo below). The vocabulary and diverse algorithms were used to foster discussion among the math students and develop a value in the students of the unique diversity found in the school and community, and an accompanying diversity in thought and mathematical action as well.

In Table 1 below, the reader can see the pluralistic mosaic found in the SDAIE classroom. About half were male and half female, with most females being either Latina or Russian/Ukraine. This researcher was primarily interested in how the students related to classroom activities, homework and materials in mathematics (algebra and pre-algebra SDAIE classrooms) three data collection techniques were used: teacher interview, observations, and individual student interviews.

Question 1: Do the algorithms we use have cognitive as well as pedagogical significance for their users? One’s mother tongue affects one’s personal form of cognitive processing (Holtz, 2001; Devlin, 2000). It appears that some language groups have significantly more incidences of dyslexia, most notably native monolingual speakers of American English. This interaction of verbal and written language, suggests that monolingual children in California possess equal difficulty with the standard algorithm as taught here, and they may also be influenced by factors related to the unique linguistic interactions between American Standard English and the algorithms taught in the United States. Could it be that this difficulty is a form of arithmetic dyslexia brought on by the unique consequences - monolingualism, in American English and our standard algorithms? Connect this to the diversity in algorithmic thinking and learning, plus the use of different measurement systems, and one can easily see that even larger differences begin to form among groups. So it is that influences of multilingualism, algorithms and measurement systems intersect in strikingly unique and interesting patterns found in students in public schooling systems. I venture to say that eventually we will see, as Devlin predicts, that certain Asian languages facilitate mathematical logic better than others and might be taught to all learners.

Once we thought that a truly educated person, had a balanced education in the classics of literature, mathematics, and spoke Greek, Latin and French along with their home language. It seems in this new age, where Latin and Greek, are less helpful than say Mandarin and Spanish, we might want to reconsider our narrow view here in the United States in relation to learning languages. This may mean that a combination of a European and an Asian languages and perhaps the use of the Franco-Brazilian method for long division may eventually form a cognitive foundation that will allow learners an added advantage as they learn more advanced mathematics. This of course needs further study.

Culture does not so much determine as influence a person’s ability or intelligence, but it can produce many different ways of knowing and learning (Johnson, 2003, p. 8). What and how we have traditionally been teaching mathematics, does not appear to work for the majority of our students. Yet at the same time, many students come to us, having learned mathematics using these very same strategies. As we continue in our mathematics reform, immigrants offer alternative tools, techniques, algorithms and ideas.

How schools anywhere in the world choose to teach the basic algorithmic operations of addition, subtraction, multiplication and division and at the same time how and what problems are placed in front of their students and for them to solve is different to some extent across cultures. At the same time, many can see that core math concepts possess a certain universality. Yet, individual abilities and inabilities differ by context, culture and socio-economic level. The work I outline here is influenced by that of Freire, (1997), D’Ambrosio (1999, 2001), Secada (2003); Perkins & Flores (2002); Philip (1996); and Zaslavsky (2001) who in their own way have assisted me to describe how the development of mathematical concepts differ, and how each of these constructions may differ across cultures and language groups.

Question 2: What is the consequence for language acquisition (multi-bilingualism) and a specific algorithm? As alluded to earlier, the greatest differences in calculation are found in long division. There are at least five major patterns used for long division, four of which have been observed in use by immigrants to Sacramento. For purposes of this study[6], they were called: North American; Franco-Brazilian; Indo-Pakistani; and Russo-Soviet. A fifth, introduced to me by a colleague in Norway, has not been found in the samples gathered from this part of the world as of this writing.

There are elements of the algorithms in our work that both delight and interest students and teachers alike. What is gained is an insight towards more than traditional ideas related to the universality of mathematics, or what many refer to as mathematics as a language. The different algorithms used by our students represent dialects in arithmetic calculation. This is no different mathematically, than those of us who speak Brazilian Portuguese, and differ slightly in pronunciation and vocabulary than the Portuguese spoken in Portugal. As Secada recommends, “Teachers need to be alert to how students think about computations”. Looking at the diversity of the algorithms found in our classrooms, allows for not only the teacher bit the students themselves to observe and value these differences. “The point is mathematical language, like language in general, develops in context to support communication (Secada, 2003, p 12).”

Finding 1: Facility with the algorithm one uses, including its unique history and cultural significance, interacts with one’s ease and ability in the language(s) one uses to communicate. Discussions that have students share their own diverse ways of mental or paper calculation, can lead to the similar discussions of solving problems. The discussion is equally enhanced by sharing and posting vocabulary of new terms in the various languages spoken by the class[7]. The multilingual students, using “Soviet” patterns performed markedly better than the monolingual students. Performance is equated with continued desire – past required California exit-exam algebra coursework. This finding places value on the importance of the interaction between our spoken languages and the algorithms we use. These combine to form individual abilities or disabilities in mathematics. Success during early attainment of arithmetic operations forms the basis for how successfully one learns advanced mathematics later in life. This is learned while students are learning their native or formal school languages.

Finding 2: Culture most certainly appears to exert a certain influence on mathematics interest and ability. Multilingual immigrants in this study are far more driven to take advantage of what the native-born students have grown accustomed to. Their boredom threshold is much higher, which appears to serve them well in relationship to standard high school classroom mathematics activities. In this school, the multilingual immigrant student naturally sees connections and differences as interesting, and appears to be able to use this background to advance in mathematics in this study. The foreign-born multilingual recently arrived immigrants are far more likely to succeed and advance in mathematics. The learning of more than one language assists in learning mathematics. Perhaps it is because, as many of us are prone to say, “Mathematics is a language”. A clearer understanding about this came about by looking at the literature in semiotics.

In reviewing the findings of what the semiotic perspective may offer towards an understanding of how natural language, mathematics, and visual representations can come together “to form a single unified system for meaning-making” (Houser, 1987). It is important to note that, like definitions of culture and ethnomathematics, there are diverse approaches to semiotics. The different points in which reflections on mathematics might be clarified by applying semiotics are worthy of a separate discussion. Briefly, semiotics looks at symbols, and how they refer to and engage language and forms of communication. It is the relationship of particular symbols and the language(s) we speak which exerts influence on mathematical thinking. Rosa (2004) outlines one theory (Pierce) in relation to icons and symbols:

Peirce’s theory of signs and his classification from the point of view of the object of the sign is helpful in understand different ways to represent the long division algorithm. Peirce defined a sign as “anything which I so determined by something else, called its object, and so determines an effect upon a person, which effect I call its representant. In this view, educator use signs all of the time, to interact with students. Peirce believed that signs are the matter or the substance of the thought and said that life itself “is a train of thought”, that is, life and signs are fundamentally related and unseparable for all human beings. Teachers present their students with signs (representants) in hopes of helping them to understand information. Sometimes mathematical lessons revolve around coming to some sort of consensus and understanding of a meaning of a sign such as the symbol for the division algorithm. Often, mathematical lessons simply use the representations to help relate other ideas or signs. Sometimes students do not see the “sign” or “symbol” or “algorithm” as teachers assumed they would. Peirce’s classification of signs from the point of view of the subject is helpful in understanding these representations, he classified the relation of a sign to its object in one of three ways: as an icon, index, or symbol. An icon has some “quality” that is shared with the object. An index has a “cause and effect link” and a “symbol” denotes its object by virtue of a habit, law, or convention”. In this context, a symbol is an abstract representation of the object.

The division symbol used by U.S., Brazilian, or Ukrainian students can most certainly be interpreted as an icon. The drawn division symbol (referred to above as the representant) looks like the “real division symbol used in schools”. By understanding the above classification model, it is understandable that mathematical representations might indeed be perceived in different ways by different students and teachers. What is an icon to teachers may be perceived as a symbol to their students. We can then realize this has many potential effects for us as mathematical educators in linguistically diverse environments. Future research will want to consider assisting teachers to learn all symbols and icons (all signs) that student’s might interpret differently - seeing the division symbol as division, and the student seeing it as the icon for square root. We might consider as well how to use this knowledge as a method in their instruction.

Perhaps one day in the future, teachers will be trained to be more diagnostic in how they work with individual student needs and abilities in mathematics. Perhaps in a future classroom we may find teachers trained in using certain combinations of languages and algorithms that were found to be optimal for increasing mental calculation. Perhaps United States students in the future will be required to learn two or three languages while gradually gaining fluency in English and the mathematics necessary for their advancement and understanding of the world around them. I saw this to some effect as a teacher of English and mathematics in Guatemala. The students in our school began learning both languages in preschool and by the time they entered the university they could fluently speak both languages and do mathematics in both languages. Again, I imagine that readers outside of the United States may find this prediction, strange if not weird. But the reader must be reminded that, despite this diversity, it is currently impossible to become bilingual under current public school curriculum in this country.

The above work has led to the establishment of the Algorithm Collection Project (ACP, 2004) at California State University, Sacramento. The ACP has initiated a systematic method that collects algorithms, and related curiosities in the basic four arithmetic operations. It has trained more than 150 hundred students and teachers in interview techniques designed to increase cultural understanding problem solving and multilingualism from with in a mathematics context. This is done in hopes that a broader catalogue of the mathematical diversity in this region, may eventually give us a clearer picture of why certain students do better than others in mathematics.

The differences we observed in arithmetic algorithms serve as cognitive cultural artifacts of the international colonial expansionary patterns of the 18^th, 19^th and 20^th centuries. I have been most privileged to see Azerbaijani and Russian students come to understand why their algorithms and math experiences are similar. I have been present when Vietnamese and Brazilians immigrants explore and learn to compare why their own are similar, yet different from that of the USA, Ukrainian or Iranian friends in the class. Having them recount to me and others about schooling experiences abroad is a great honor for me. When an Iranian immigrant shares how he was excluded from attending school in his city and had to flee his country because he and his family are members of the Bahá’í Faith, or a Bosnian student talks about schooling and war, the context of what is hard and difficult for us here can change marketedly.

My preservice and practicing public school teachers involved in ACP work have also come to see the patterns of why some groups use one algorithm as we alluded to above. When teachers see students using different forms of addition, subtraction, multiplication or division, they are better equipped to ask about the culture, classroom experience in their home country, and other personal details that allow all students to feel welcome in the classroom. One teacher at an ACP in-service shared with me the following:

I was surprised to find that common day-to-day algorithms differ by culture and by national origin. At first I assumed that these differences were minor and of relatively little significance. I am convinced now that they represent a foundation that adds up, not only in individual students, but may indeed be generalizable to cultural groups.

Generalizability in this case is problematic, if not premature but a pattern exists none the less. The advantage of interviewing newly arrived adolescent immigrant students in relation to how they learned basic mathematics facts and algorithms is that the experience is still fresh for them. These interviews allow one to gain a limited perspective about what is actually happening now in schools that one cannot visit. To date, the ACP has completed one ethnography related to Vietnamese mathematics (Orey and Nguyen, 2003). Further ethnographies of Guatemalan, Brazilian, Russian/Ukraine and Iranian mathematics are nearing completion. As each one is completed, they are placed on the Algorithm Collection Project website (ACP, 2004).

What I have outlined here is my own journey. It is my own attempt at describing what seems to work for a highly diverse population as found here in Northern California. Our abundant diversity is, by all means, a leading factor in the development of our highly eccentric, dynamic and highly creative society. From both a pedagogical and ethnomathematical perspective, the diversity found in our classrooms is a useful tool and not a problem to be overcome. Many of our traditional deficit models of multiculturalism force diverse elements of our society to conform to a mainstream model (Payne, 1998). We have traditionally sought to bring diverse groups of people into line with the mainstream culture and curriculum, yet have done little to encourage the mainstream culture in the learning of and learning from the diversity, languages and experiences brought to us by newly arrived of immigrants. This seems a sobering loss of opportunity (Lindsey et al, 2003) and one that the ACP seeks to ameliorate through extended research.

So it was that, on that day when I observed the Ukrainian student struggling with her new understanding of the division symbol in the problem, I was seeing what Houser (1987) observed, “The interpretant related to this representant of the division symbol was different for the student than for this teacher. I, being the teacher (interpretant) was using the division symbol to represent a division algorithm, while the young lady from the Ukraine viewed the division icon representing a square root and asked for a calculator. Neither of us knew what a remarkable moment it was for the both us.


Russia	6	Most have studied Russian, Ukrainian, English and German	2 male, 4 female
Ukraine	6	Most have studied Ukrainian, Russian, English and German	3 male, 3 female
Hispanic	10	Most have studied Spanish	2 male, 4 female
Brazilian	1	Portuguese and Spanish	female
Marshall Islands	1	English, Marshallese	male
Liberia	1	English	male
Samoa	1	English, Samoan	male
India	2	English, Punjabi	Both male
Pakistan	1	English, Urdu, Punjabi	male
China	1	Cantonese	female
Serbia	3	Serbian, French	male

Armas, G. C. (2003, Thursday, October, 9). I in 5 Americans don’t speak English at home. The Sacramento Bee, p. A9.

CDE. (1999). Mathematics Framework California Schools. Sacramento: California Department of Education.

D'Ambrosio, U. (2001). "What is ethnomathematics, and how can it help children in schools?" In: Teaching Children Mathematics, 7(6). Reston, VA: National Council of Teachers of Mathematics.

_____________. (1999). Educação para uma sociedade em transição (Education for a Society in Transition). Campinas, SP, Brazil: Papirus Editora.

Devlin, K. (2000). The Math Gene: How mathematical thinking evolved and why numbers are like gossip. Basic Books.

Freire , P. (1997). Pedagogia da Autonomia: Saberes Necessários à Prática Educativa (Pedagogy that Gives Autonomy: Necessary understandings towards a practical education). São Paulo: Editora Paz e Terra.

Holtz, R. L. (2001, March 16). “Study: Some written languages intensify dyslexia.” The Sacramento Bee, p. A20.

Houser, N. (1987). “Toward a Peircean Semiotic Theory of Learning Semiotics.” The American Journal of Semiotics. pp 249–74.

Johnson, L. M. (2003). Culture and Learning. Arlington, VA: Educational Research Service.

Lindsey, Robins & Terrell (2003). Cultural Proficiency: A manual for school leaders, Second Edition. Thousand Oaks, CA: Corwin Press.

Luitel, B. C. (2002, November 28). “Representation of mathematical learning: A short discourse”. Paper presented at Presented at the 25th conference organised by Western Australian Science Education Association on 28 November 2002 at Canning College Bentley. Curtin University of Technology: Australia. Found at: http://www.bcluitel.mysitespace.com/Seminar.htm

Orey, D. & Nguyen, K. T. (2003). “The Ethnomathematics of Vietnamese Algorithms”. NASGEm: North American Study Group on Ethnomathematics Newsletter. 1(2).

Orey, D. & Rosa, M. (2003, setembro) Vinho e Queijo: Etnomatemática e Modelagem. BULEMA - Boletim de Educação Matemática. Unversidaded Estadual Paulista – Rio Claro, Brasil.

Orey, D. & Rosa, M. (2002). Fasciculo Didático (text) Ciências de Natureza e Matemática: Modelação Algébrica. and (2003). Fasciculo Didático (text) Ciências de Natureza e Matemática: Trigonometria: Linguagem e Instrumento. Escolas Associadas Pueri Domus: São Paulo.

Payne, R. K. (1998). A framework for understanding poverty. Highlands, TC: Aha! Processing, Inc (www.rubypayne-poverty.com).

Perkins, I. & Flores, A. (2002, February). “Mathematical notations and procedures of recent immigrant students”. Mathematics Teaching and the Middle School. Reston, VA: NCTM. (7)6. pp 346-351.

Philip, R. (1996, November). “Mathematical notations and procedures of recent immigrant students”. Teaching Children Mathematics. Reston, VA: NCTM. pp 128-133.

Rosa, M. (2004). A Mathematical Taboo: Mathematics as Universal Language. Unpublished manuscript available form the author.

Secada, W. G. (1983). The educational background of limited-English-proficient students: Implications for the arithmetic classroom. Arlington Heights, IL: Bilingual Education Service Center. (ERIC Document Reproduction Service No. ED 237318)

Zaslavsky, C. (2001). “Developing number sense: what can other cultures tell us?” Teaching Children Mathematics. Reston, VA: NCTM. Vol. 7, No. 6, 312-319.

[1] Specially Designed Academic Instruction in English (http://www.rohac.com/sdaieinfo.htm)

[2] The school has onsite translators in Russian, Ukraine, Spanish, and Cantonese.

[3] A recent article (Armas, 2003) has highlighted that in fact 1 in 5 United States residents do not use English in the home.

[4] Few Ukraine or Russian immigrants have met Brazilian, African-Americans or Mexican-Americans for instance

[5] With this diversity, the near impossibility of becoming bilingual in most parts of the United States, a concept that is hard to grasp by readers who live out side of North America.

[6] I collaborated with the students and classroom teacher and developed the names for these, as they are related to the patterns they saw as well

[7] See the Algorithm Collection Project's Virtual Vocabulary Wall at: http://www.csus.edu/indiv/o/oreyd/ACP.htm_files/vocabwall.htm

Franco-Brazilian	USA	Russo-Soviet