Working Title: The Ethnomathematics of Vietnamese Algorithms

Daniel C. Orey & Kieu T. Nguyen

California State University, Sacramento

This paper represents the second in an ongoing series of research findings related to the Algorithm Collection Project at California State University, Sacramento. It is the goal of this paper to outline the mathematics education of children from Vietnam. As well, we outline what we have found as a unique difference in the instruction in mathematics that allows many Vietnamese, and Vietnamese-American students to be successful in math as compared to their non-Vietnamese peers. This discussion briefly reviews the educational system in Vietnam and offers a contrast in the way mathematics is approached in Vietnam and in California. Included as well, in this work is an outline of algorithms that are used by recently arrived Vietnamese immigrants.

Historical Background

Many foreign countries have influenced the Vietnamese educational system, with the Chinese and the French making the greatest impact of all in the shaping of the current academic structure in Vietnam. Initially, Vietnam adapted a model rooted in the Chinese schooling based on Confucian philosophy, emphasizing educational attainments and ritual performance. During the time as colonizers of French Indochina, which included current Vietnam, the French laid a foundation for the current structure of the Vietnamese education system by developing a system from preschool education to higher education common to France and other former French colonies. At this time elementary schools consisted of only one or two grades of primary education. Whereas, the Chinese were selective in who was educated, it was during this period the overall system expanded to allow a broader range of the population to attend school.

The Vietnamese educational system of the French Indochinese colonial era ended when North Vietnam became an independent nation in 1954. Nevertheless, the French influence in the current Vietnamese school system is still evident. In what was once called North Vietnam, there were two educational systems: the old one, which is similar to the French twelve year system, and the new one consisting of a nine year system (Sloper & Can, 1995). Prior to the end of the Vietnam War, South Vietnam was controlled by the Saigon regime where the education system remained the same as the French system. After the war, and in order to effectively unify both the North and South, the two school systems were merged and became a new ten-year system. In 1975, a twelve-year education system was put into place due to a major educational reform, and all children began school at the age of six. The structure of the educational system in Vietnam today can be summarized as follows (Do, 2003):

Age	Year/Grade
22 +	Colleges, Universities
21 +
20 +
19 +
18 +
17 +	12 11 Senior Secondary School 10
16 +
15 +
14 +	9 8 Junior Secondary School 7 6
13 +
12 +
11 +
10 +	5 4 3 Primary School 2 1
9 +
8 +
7 +
6 +
5 +	‘Young Shoot’ education

Primary school: Children from 6 years of age are admitted to this level and their age is calculated according to the year of birth. Grade 1 is the first grade of primary education, which includes grades 1 – 5.

Junior secondary schools: Children from the age of 11, consists of three years (grades 6 – 9).

Senior secondary schools: Children from the age of 15 and consists of three grades (grades 10-12).

Higher education: (college, universities and postgraduate education): Course of study is 3 years for college, 4 to 6 years for universities. To receive a MA degree, an individual needs to have graduated from a university; the study is 2 years. For a Doctoral degree, the study is 3 – 4 years or more.

The universalization of primary education in Vietnam was a major policy of the Vietnamese State throughout the past 50 years. However, it was in 1989, that the Vietnamese government publicized the law on the universalization of primary education which emphasized the state’s commitment to a required and free primary education for all children in the country. In this plan, there are two main types of schools:

(1) state schools organized by the state (98 % of the pupils attend these schools) and

(2) private schools which are organized and managed by individuals (Do, 2003). In both systems, students are given instruction under a strict environment.

Both Do (2003) and Phung (2003) have described that in Vietnam, the majority of teachers use a very rigid or standardized teaching style as compared to that common in the United States. Concepts are taught first, followed by a great deal of practice with less emphasis on context. The teacher spends 99% of class time using highly structured lessons used to complete daily objectives. Often learning is accomplished through the use of homework.

In the primary classroom, students are seated in rows. Typically the mathematics lesson time consists of 90% of whole class teaching when the teacher places emphasis on the explanation of illustrated methods to the whole class; 8% is devoted to individual work and 2% to group work (Do, 2003). During each math lesson, pupils take turns at working at the board in front of the entire class. Students’ mistakes are usually dealt with individually. Basic operations like addition and multiplication facts are learned by heart. Students are required to solve basic algorithms through the use of mental math strategies which we will attempt to explain later in this discussion.

Assessment

Students in Vietnam must pass a comprehensive examination prior to entering junior secondary, senior secondary and university. In addition, at the end of each grade level the students are administers end of the year tests and must score at least 70 percent to move to the next grade. The first major exam is at the end of primary school, which is year three (age 9). It is a comprehensive test that covers the first three years of schooling in the subjects of mathematics and Vietnamese. The next exam comes at the end of year five when students are in grade 9. This examination covers six subjects, and is concerned with the mastery of material from grades 6 to 9. When students complete grade 12, they take a required comprehensive examination including all materials covered in grades 10 to12. Once students pass this test, they are granted a “Certificate of Lower Secondary School”. This is equivalent to a high school diploma in the United States. If students wish to pursue higher education, then they must take either a National Examination to attend college or the Entrance Examination for the National University of Hanoi. Both tests are usually taken by the age of 18.

Vietnamese immigrants tell us that it appears that the content of the Vietnamese Educational system is more rigorous than that found in the United States. Vietnamese schools do not allow every student to pass and move on to the next grade level unless they can demonstrate mastery of the material. The problem is that a great number of students drop-out before entering high school. Those who live in rural areas are less likely to finish sixth grade because of poverty and access to schools, despite the overwhelming aspect of Vietnamese culture which values those who are educated. Educated people are to be well-respected as they have proven to the population that they have demonstrated the ability to succeed and overcome an extensive and rigorous schooling experience. Related to this is another important aspect of the Vietnamese school system; students study extremely hard and are respectful of their teachers.

The factors that have been outlined above contribute toward success in Vietnamese children in math (i.e. mental calculation, hard study, and the overwhelming value placed-on education). It appears from our research, that the Vietnamese education system does not make it possible for every student to be successful, only the “smart and quick” kids are able to take advantage or overcoming the system. As for the poor, or those who need some form of extra assistance, these students are left behind and drop out of school.

Calculation and Algorithms

The cultural aspects of schooling and language as described above indicate to us that the process of learning mathematics in Vietnam is different from that found in the United States. We would like to turn now to descriptions of the use of traditional Vietnamese algorithms.

In the United States, when working through an algorithm problem, one is taught to (and the majority of people continue to) write out most every step of the procedure on paper. “Show your work” is a common refrain in many classrooms in the United States, with the outcome of showing your work continuing on throughout adult life in most extensive calculations made without a calculator. However, solving basic math operations requires Vietnamese students to rely upon mental calculation. Adults encourage students not to write every single number on the paper, but to rely upon mental calculation instead.

Let us look at some of the examples of the process by which Vietnamese students solve the basic algorithm of addition, subtraction, multiplication, and division compared to the method commonly found in the United States.

ADDITION:

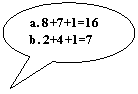Vietnamese’s Method United States Method

1 1

2 8 7 2 8 7

+ 4 7 3 + 4 7 3

7 6 0 7 6 0

The process of solving a multi-digit addition problem in Vietnam, as in the United States starts out by adding the ones column. 7 added to 3 gives you 10. Then one puts a 0 in the ones column underneath the line and it is not required to carry the one over the tens column, as in the United States. Repeating this process in the 10’s column, one mentally adds 8 + 7 and then adds the 1 that was carried over from the ones column, which gives 6. Finally move to the hundreds column and again mentally add 2 + 4 plus 1 (carried over from the tens column) to get 7. Notice that the carrying over is not written down. Students are taught to remember that a number was carried over to the next column and was added in when calculating the other numbers mentally.

SUBTRACTION:

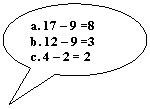Vietnamese’s Method United States’ Method

3 11

4 2 7 4 2 7

- 1 8 9 -1 8 9

2 3 8 2 3 8

In using the Vietnamese method, one starts in the one’s column and begins by subtracting 9 from 7. But 7 is not big enough, so one borrows ten from the 2 on the tens column which will then give 17. Now “mentally take away” 9 from 17 to obtain 8. Then add 1 back to the 8 on the tens column to get 9 and mentally subtract 9 from 2. Again 2 is too small to subtract 9 so borrow another ten from the hundreds column. You now have 12 minus 9 to get 3. Now, move to the hundreds column and return 1 to the 1 in the hundreds column to get 2. Then mentally subtract 2 from 4 and get 2. Your final answer is 238. The differences between the Vietnamese method and the method as traditionally taught in the United States of doing subtraction seems to be that Vietnamese calculation borrows from the ten from the top number but returns 1 back to the bottom number. In the U.S., borrowing is undertaken and returned only at the top. Vietnamese subtraction does not pencil-in what they borrow nor make a cross mark to indicate a number that has been borrowed because those steps are done mentally.

MULTIPLICATION

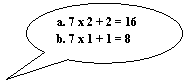Vietnamese’s Method United States’ Method

1 2

1 2 3 1 2 3

x 7 x 7

8 6 1 8 6 1

The Vietnamese process of multiplying is similar to that of addition and subtraction discussed above as students are still required to do mental math. Begin by multiplying 3 and 7 to get 21 then put the 1 under the line, but do not write the 2 over the 2 on the tens column (don’t carry the 2 over). Next, multiply 2 and 7 in your head and add 2 that you mentally carried-over from the previous calculation to get 16. Write the number 6 in the tens column underneath the line and disregard writing the 1 that needs to be carried over. Then you multiply 7 and 1 then add 1 in your head to get 8. In this method the only number written is the answer and you don’t write the numbers that are carried over to the next column. Finally, to make sure the answer is correct, Vietnamese mathematics involves an interesting checking algorithm for correctness.

1 2 3 (a)

x 7 (b) (a) 6

8 6 1 (d)

(d) 6 (c) 6

(b) 7

1. Start by drawing an X.

2. Locate (a) in the multiplication problems, which is the top number and add all three digits, which are 1, 2, and 3 to get 6. Write that number in the space that is labeled (a) in the X.

3. Then add up all the digits indicated by the (b) which is only one digit the number 7. Write that number on the bottom of the X labeled (b).

4. Now multiple the numbers in the space of (a) and (b) in the X, which is 6 and 7 to get 42. Then add the product of (a) and (b) which is 4 + 2 = 6. Write the number 6 in the X labeled (c).

5. Finally, you want to add all the digits of the answer labeled (d) from the problem above, which are 8, 6, 1 and you, get 15. Then add the 2 digits of your sum that is 1 +5 =6. Write the 6 in the space labeled (d) in X.

6. If the numbers from (c) and (d) are the same then the answer you got from the original problem is correct. In this case (c) = 6; and (d) = 6, the two answers match.

DIVISION:

Vietnamese method U.S. method

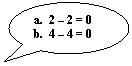
24 2 1 2

04 12 2 2 4

0 - 2

0 4

- 4

0

In Vietnamese, the division bar is drawn differently from that used in the United States. The Vietnamese adopted this symbol from the French where the bar is upside down and backwards as compared to the standard U.S. algorithm. The process of division starts out by having the students think to themselves how many times 2 (divisor) goes into 2 of the number 24 (dividend). The answer is 1, so you write the number on the right side of the problem underneath the line where the divisor 2 is located. Then again think to yourself 2 minus 2 is 0 so you put the 0 under the 2 of the number 24. Next move over to the 4 and think to yourself “how many times does 2 go into 4?” which is 2. Write the 2 next to the 1 under the line. Again think 4 – 4 is 0 and you put the 0 under the 4 of the number 24. Your answer is 12, which is written on the bottom of the divisor.

Checking your answer

(c) 24 2 (a) (a) 2

12 (b)

(c ) 6 (d) 6

(b) 3

1. As in multiplication, draw a big X.

2. Write the number indicated by (a) from the division problem to the space labeled (a) in the X which is 2.

3. Add up the two digits of the quotient, which is 12 (1 + 2) to get 3. Write this number in the space labeled (b) in the X.

4. Add the two digits 24 (dividend) together which is labeled (c), so you get 2 + 4 = 6. Write 6 in the space labeled (c) in the X.

5. You multiply the number from (a) and (b) which is 2 and 3 to get 6. Place the number 6 in the space labeled (d) in the X.

6. If the number from (c) and (d) are the same then the answer is correct.

Conclusion

Ms. Nguyen, a Vietnamese-American, and co-author grew up in the United States and has said “unfortunately my parents did not educate me about Vietnamese educational practices that they experienced.” Prior to this investigation her personal conceptions about Vietnam were negative, and she pictured the country as one that did not put a very high value on education. In her mind, many people of Vietnamese heritage could not advance very far (including her parents) in Vietnam. From them, she heard numerous anecdotal stories about people in Vietnam who often quit school because they could not afford the fees, and whose parents needed their children to help at home. But this was only the case as demonstrated by poor village residents when her parents were still in Vietnam, twenty or more years ago.

What we found is that now there is an increased value on education both here in the United States amongst Vietnamese-Americans and in Vietnam. Education appears to be valued even more than before (by people of Vietnamese heritage living in both California and in Vietnam), and poor children are able to complete high school in ever growing numbers in Vietnam (Phung, 2003). From a review the limited literature, and interviewing recently arrived immigrants about Vietnamese education, we learned that an increasing number of people are attending school in Vietnam and are now able to go on to university. We also found that there are numerous colleges and universities being constructed in Vietnam for specific professions and trades.

As an American of Vietnamese background educated in the United States, Ms. Nguyen was just as fascinated as Professors Orey and Professor Phung to learn about and share the different approaches people in Vietnam and the United States use to solve addition, subtraction, multiplication, and addition problems. She stated, “I am so used to the American way that when I tried solving it (the Vietnamese method) myself I sometimes got confused, especially with the division procedure. I feel very fortunate to learn a new way to approach basic algorithms.” Ms. Nguyen learned to value education very early in her life from her parents. As she has said, her “mother and father came to United States to better their lives and build a brighter future for their children.” Through her years of schooling she had her parents’ support and they supported her and encouraged her to do her best. She stated, “I think Asian children do well in school because they are hard working and have the persistence to keep trying and to not give up easily.”

Through a study of the basic algorithms and procedures as used in Vietnam, we have come to realize that the emphasis of mathematics is on the construction of a strong repertoire of mental mathematics. By calculating mentally, Vietnamese students are as both Nguyen and Phung have described as “exercising their brains”. This type of instruction encourages students to use and rely upon their own memory (internal resources) and allows students to fully understand how to calculate basic algorithms. Children in Vietnam are taught two-digit multiplication as early as second grade whereas children in the United States learn multiplication more than a year later, around third grade. Another factor that may contribute to the ability to develop “rigorous” mathematics in Vietnam, is that students are expected to retain all concepts learned from grade one and on, in preparation for comprehensive examinations which allow students to move to the next grade.

The Algorithm Collection Project[i] by using an ethnomathematics-based pedagogy is interested in studying the observable linkages between how particular algorithms are used, what and how many languages are spoken, and the internalization for the mathematics used by an individual.

Bibliography

Do, Dat. (n.d). Mathematics teaching and learning in Vietnam. Retrieved on March 14,

2003 from http://www.ex.ac.uk/cimt/ijmtl/ddvietmt.pdf

Sloper, David & Can, Le T. (1995). Higher education in Vietnam: Change and response.

New York: St. Martin’s Press.

Q. Phong, personal communication, March 14, 2003.

Acknowledgements

The authors greatly appreciate the feed back from Charlie Carroll at the University of California, Berkeley. Quoc Phung, Pamela Milchrist and Vicki Pearson-Rounds at California State University, Sacramento, and Ubiratan D’Ambrosio in São Paulo, Brazil

---

[i] http://www.csus.edu/indiv/o/oreyd/ACP.htm_files/Alg.html